4-6座標軸の調整

---

このページの内容

1. 座標軸をずらす
2. 座標軸をずらす例1
3. 座標軸をずらす例2
4. 座標軸をずらすアニメーション
5. アニメーションで座標を変更する際の注意点
6. 座標を回転する
7. 座標を回転する例1
8. 座標を回転するアニメーション
9. 座標を回転する例2（失敗例）
10. 座標を回転する例3（成功例）
11. 座標の記録pushMatrix()とpopMatrix()
12. pushMatrix()とpopMatrix()を使った例1
13. pushMatrix()とpopMatrix()を使った例2
14. pushMatrix()とpopMatrix()を使った例3
15. scale()による座標の拡大や縮小
16. 座標の拡大、縮小の例1
17. 座標の拡大、縮小の例２　対象を大きくする
18. 円を拡大するアニメーション。
19. 円を拡大するはずが、失敗する例
20. クマさんを大きくするアニーメーション
21. クマさんの大きさとともに位置も変えるアニーメーション

---

座標軸をずらす

通常の状態では、座標軸は画面の左端上端が原点に設定されていますが、これを自由に変更することができます。
座標をずらすには、translate()という命令を使います。パラメーターは、x軸上の座標移動値、y軸上の座標移動分です。

translate(x軸上の座標移動分 , y軸上の座標移動分);

---

座標軸をずらす例1

まずは簡単な例で、感覚をつかみましょう。下記の例では、画面の中心に二つの円を描きます。しかしながら、初めの円は通常の座標軸上でかき、次の円は座標をずらしてから描きます。ずらす量は、x軸方向、ｙ軸方向ともに画面サイズの四分の一です。

size(400,300);
ellipse(width/2,height/2,30,30);
translate(width/4,height/4);
ellipse(width/2,height/2,30,30);

結果は下記になります。画面中央の円は、通常の座標で描かれたものです。画面右下の円は、座標をずらしてから描かれたものです。

---

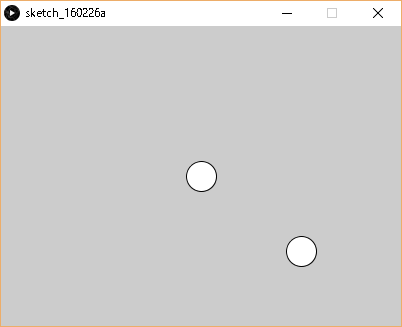
座標軸をずらす例2

上記の例をわかりやすくするために、line()を使って補助線を引いたり、円に色を付けたりします。

size(400, 300);
for(int i=0; i < width; i+= width/4){  //補助線を書く処理
  line(i,0,i,height);
}
for (int i=0; i<height; i+=height/4) {  //補助線を書く処理
  line(0,i,width,i);
}

fill(255,0,0);
ellipse(width/2, height/2, 30, 30);
translate(width/4, height/4);
fill(0,255,0);
ellipse(width/2, height/2, 30, 30);

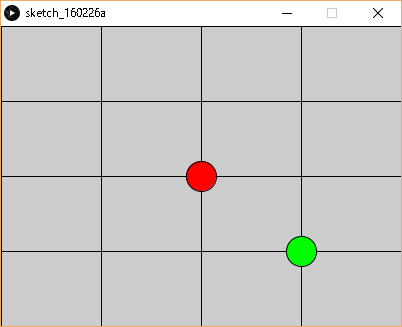
結果は下記になります。
座標を移動してからの円が緑色の円です。ひとつ目の円もふたつ目の円もellipse()に指定するパラメーターは同じです。しかしながらも、translate()によって座標が変わるため、円が表示される位置が変わるのです。

---

座標軸をずらすアニメーション

では座標が変わる様子をアニメーションで表現してみましょう。
下記では、座標移動により円が移動します。線が交差しているのが原点です。原点とともに、円が移動します。

int tx=0;  //x軸上の座標の移動分を格納する変数
int ty=0;  //y軸上の座標の移動分を格納する変数

void setup() {
  size(400,400);
  fill(255, 0, 0);

}

void draw() {
  background(200,200,200);
  translate(tx,ty);  //座標を動かす
  
  line(-width*10,0,width,0);  //原点のx軸上に線を引く
  line(0,-height*10,0,height);  //原点のy軸上に線を引く
  
  ellipse(0, 0, 30, 30);

  tx++;
  ty++;
}

上記コードは下記のように動作します。

座標を移動させるだけなら、その結果には何も目新しいことはありません。ただ物体が移動するだけです。座標移動は、これから説明する座標の回転や、座標の拡大や縮小のために必要不可欠な技術なのです。

---

アニメーションで座標を変更する際の注意点

座標を移動させる際は、フレームごとに座標が初期化される（draw()による繰り返し処理のたびに原点の位置が左端上端に戻る）ことに注意してください。

---

座標を回転する

座標を回転するにはrotate()という命令を使います。パラメーターでは、座標をどれだけ回転するかを指定します。この指定では、ラジアンという単位の数値を用います。ラジアンは弧度法という単位です。下記に度からラジアンへの変換式を記述します。
ラジアンの値　=　度での値　＊　円周率　÷　180

rotate(ラジアンで指定する座標を回転する量);

---

座標を回転する例1

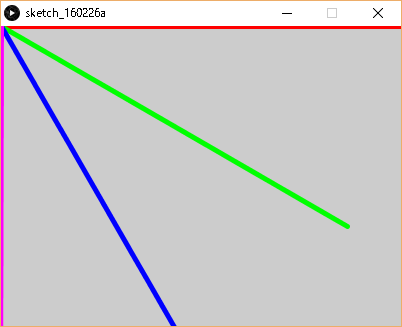
下記の例では、原点から真横に線を引く処理を四回繰り返しました。ただし、線を引く度に座標を30度ずつ回転させます。初めの線（通常の座標系で描かれる線）は、赤色。30度ずらして描かれた線は黄緑、さらに30度ずらして描かれた線は青色、もう一度30度ずらして描かれた線はピンクです。
円周率（3.1415926...）を使うにはプロセッシングでは「PI」という変数を用います。

size(400,300);
strokeWeight(5);

stroke(255,0,0);
line(0,0,width,0);

rotate(30*PI/180);
stroke(0,255,0);
line(0,0,width,0);


rotate(30*PI/180);
stroke(0,0,255);
line(0,0,width,0);

rotate(30*PI/180);
stroke(255,0,255);
line(0,0,width,0);

結果は下記になります。

---

座標を回転するアニメーション

ではアニメーションで座標が回転する例を作ってみましょう。下記では、画面左上端を中心に赤い線が回転します。

int deg=0;  //座標の回転分を格納する変数

void setup() {
  size(400, 300);
  strokeWeight(5);
  stroke(255, 0, 0);
}

void draw() {
  background(200,200,200);
  
  rotate(deg*PI/180);  //座標を回転する
  line(0, 0, width, 0);  //原点から真横に線を引く（その座標系で）
  deg++;  //繰り返しのたびに、座標の回転量を増やす
}

上記コードは下記のように動作します。

フレームごとに座標が初期化されるのは、rotate()で座標を回転させる場合も同じです。注意しましょう。

---

座標を回転する例2（失敗例）

時計のように画面中心を軸に線を回転させる方法を説明します。ただし、下記はそれをやろうとして失敗してしまった例です。その理由を考えてみましょう。

int deg=0;

void setup() {
  size(400, 300);
  strokeWeight(5);
  stroke(255, 0, 0);
}

void draw() {
  background(200,200,200);
  
  rotate(deg*PI/180);
  line(width/2,height/2 , width, height/2 );

  deg++;
}

上記コードは下記のように動作します。

このプログラムが意図した通りに動かないのは、座標の回転軸が画面の中央ではなく、画面の左端上端になっているからです。画面の中心を軸にするには、座標を回転させる前に、tranlate()を使って原点の位置をずらしておかねばならないのです。

---

座標を回転する例3（成功例）

下記が、画面中心を軸に線が回る例です。draw()の中で、translate(width/2,height/2);で原点を画面中央に移動してから、rotate((PI/180)*deg);で座標を回転させています。

int deg=0;
void setup() {
  size(400,300);
  strokeWeight(10);
  stroke(255,0,0);
}

void draw() {
  background(200,200,200);
  
  translate(width/2,height/2);
  rotate((PI/180)*deg);
  line(0,0,width/2,height/2);

  deg++;
}

上記コードは下記のように動作します。

---

座標の記録pushMatrix()とpopMatrix()

pushMatrix()は、現在の座標を保存するための命令です。popMatrix()は保存した座標を取り出す命令です（現在の座標を、取り出した座標に置き換える）
pushMatrix()が座標の情報を保存する先は、スタックというデータ構造になっています。スタックは先入れ後出しのデータ構造です。複数のデータを保存できますが、保存したデータを取り出す際の順序は保存時とは逆になるデータ構造です。pushMatrix()を連続して使用し、複数の座標を格納した場合、popMatrix()でその座標を取り出すときは、最後に格納した座標が最初に出てくるということです。使用時には注意してください。

---

pushMatrix()とpopMatrix()を使った例1

pushMatrix()とpopMatrix()を使うと、複数の地点を中心にして、座標を回転することができるようになります。下記はその例です。赤い線は、画面の左から四分の一の部分を中心に回転し、緑の線は、画面の右から四分の一の部分を中心に回転します。

int deg=0;
void setup(){
  size(400,300);
  strokeWeight(10);
}

void draw(){
 background(200,200,200);
  
//赤い線を書く処理
 stroke(255,0,0);
 pushMatrix();  //通常の座標を保存
 translate(width/4,height/2);  //座標変換処理。赤い線の中心を原点にする
 rotate(deg*PI/180);  //座標回転処理。上記で変換した原点を中心に、座標を回転する
 line(0,0,width,0);  //座標を回転した状態で線をかく
 popMatrix();  //通常の座標に戻す

//緑の線を書く処理
 stroke(0,255,0);
 pushMatrix();  //通常の座標を保存
 translate(3*width/4,height/2);  //座標変換処理。緑の線の中心を原点にする
 rotate(deg*PI/180);  //座標回転処理。上記で変換した原点を中心に、座標を回転する
 line(0,0,width,0);//座標を回転した状態で線をかく
 popMatrix();  //通常の座標に戻す

 deg++;
}

上記コードは下記のように動作します。

---

pushMatrix()とpopMatrix()を使った例2

速度の違う三つの線が回ります。上記のプログラムでは、赤い線を書く処理と、緑の線を書く処理は処理内容が似ています。下記では、共通の処理を関数にまとめました。

int deg1=0;
int deg2=0;
int deg3=0;
void setup() {
  size(400, 300);
  strokeWeight(10);
}

void draw() {
  background(200, 200, 200);

  stroke(255, 0, 0);
  drawLine(width/4, height/4,deg1);

  stroke(0, 255, 0);
  drawLine(3*width/4, height/4,deg2);

  stroke(0, 0, 255);
  drawLine(width/2, height/2,deg3);

  deg1++;
  deg2+=2;
  deg3+=3;
}

void drawLine(int x, int y,int deg) {
  pushMatrix();
  translate(x, y);
  rotate(deg*PI/180);
  line(0, 0, width, 0);
  popMatrix();
}

上記コードは下記のように動作します。

---

pushMatrix()とpopMatrix()を使った例3

上記をさらにアレンジして、三角形をゆりかごのように動かしてみました。
下記プログラムのミソはaddという変数です。addという変数は、ゆりかごの角度が高くなると、ゆりかごが逆方向に進むように符号（プラスマイナス）を切り替えています。

int deg=30;
int add=1;

void setup() {
  size(800, 600);
  colorMode(HSB, 360, 100, 100, 100);
  noStroke();
}

void draw() {

  background(359, 0,99);

  sannkaku(width/2,height/4,0,deg);
  sannkaku(width/4,height/2,100,deg);
  sannkaku((width/4)*3,height/2,200,deg);

  deg+=add;
  if(deg>60){
    add = -1;
  }
  if(deg<-60){
    add = 1;
  }
}
void sannkaku(int x, int y,int col,int deg) {
  fill(col, 99, 99, 50);

  pushMatrix();
  translate(x, y);
  rotate((PI/180)*deg);
  triangle(0,0,-width/4,height,width/4,height);
  popMatrix(); 

}

上記コードは下記のように動作します。

---

scale()による座標の拡大や縮小

座標を拡大させたり縮小させたりすることができます。自分で作成したキャラクターを大きくしたり小さくしたりといったことをしたい場合、とても便利です。
座標の拡大縮小にはscale()という命令を使います。パラメーターには数値を与えます。例えばscale(2.0)とすると、座標が倍になり、描いたものが倍の大きさで表示されるようになります。sclae(0.5)とすると、座標は２分の１に小さくなり、描いたものが半分の大きさで表示されるようになります。

scale(数値);

---

座標の拡大、縮小の例1

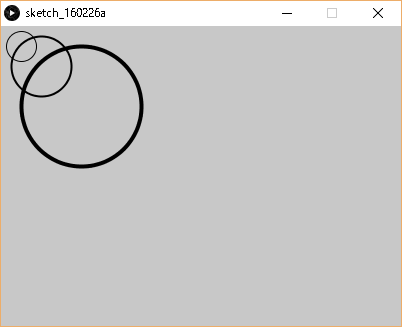
まずは簡単な例で感覚をつかみましょう。下記の例では、座標（20,20）を中心として半径15の円を三度描きます。しかしそのたびにscale(2)として座標を二倍に拡大するため、円の大きさとともに中心も変わります。初めの円は通常の座標系で描かれ、中心が（20,20）で半径は15です。次に描かれる円は座標が倍になるため、通常の座標系でいうと（40,40）の位置が中心で、半径は通常の座標系での30になります。三つ目の円は、座標が通常の四倍になるため、通常の座標系でいうと（80,80）の位置が中心で、半径は通常の座標系での60になります。
座標の回転のときと同様、座標の拡大、縮小も原点を中心に行われます。つまり原点を元に座標が引き伸ばされたり、縮小されたりするのです。そのため、座標を拡大すると円が大きくなるとともに、円の中心(20,20)の位置も変わるのです。

background(200,200,200);
size(400,300);
noFill();
ellipse(20,20,30,30);
scale(2);
ellipse(20,20,30,30);
scale(2);
ellipse(20,20,30,30);

---

座標の拡大、縮小の例２　対象を大きくする

上記の例では、円を大きくすると円の中心位置も変わってしまいました。円の中心を変えずに対象を大きくするにはどうすればよいでしょうか？　その答えは、座標の回転のときと同様です。座標の原点を移動させてから、座標を拡大、縮小させればいいのです。
下記は、円を大きくする例です。原点を円の中心に設定してから座標を拡大することで、円がずれることなく大きくなります。

background(200,200,200);
size(400,300);
noFill();
line(0,height/2,width,height/2);
line(width/2,0,width/2,height);

translate(width/2,height/2);  //画面の中央を原点にする。
ellipse(0,0,20,20);
scale(2);
ellipse(0,0,20,20);
scale(2);
ellipse(0,0,20,20);

結果は下記のようになります。

---

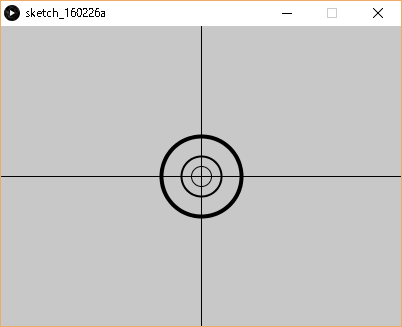
円を拡大するアニメーション

円がどんどん大きくなるアニメーションです。

float sc = 1.0;
void setup(){
 size(800,600); 
  
}

void draw(){
 translate(width/2,height/2);
 scale(sc);
 ellipse(0,0,10,10);
 sc *=1.01;
}

上記コードは下記のように動作します。(画面が真っ白の場合、拡大された円が画面全体を塗りつぶしている場合があります。その場合は、画面を長押しして、プログラムを再起動してみてください。)

---

円を拡大するはずが、失敗する例

対象物を拡大する際、その中心に原点を移動することを忘れるとわけのわからないバグが発生します（意図したとはまるで違う動作がおきてしまいます）。下記はその例です。画面の中心に円を描いているのですが、scale()のたびに画面の左上端を原点に座標が拡大されていくため、円が拡大する間もなく円の中心がずれていき、結果、円が拡大するのではなく移動したように見えてしまうのです。

float sc = 1;
void setup(){
 size(800,600); 
  
}

void draw(){
 scale(sc);
 ellipse(width/2,height/2,10,10);
 sc *=1.01;
}

上記コードは下記のように動作します。

---

クマさんを大きくするアニーメーション

それでは、クマさんを拡大するプログラムです。

float sc = 1;
void setup() {
  size(800, 600);
}

void draw() {
  translate(width/2, height/2);
  scale(sc);
  kumasan();
  sc *=1.01;
}
void kumasan() {
  fill(198, 59, 6);  //茶色
  ellipse(0 - 50, 0 -60, 60, 60);  //左耳
  ellipse(0 + 50, 0 -60, 60, 60);  //右耳
  fill(250, 111, 96);  //ピンク
  ellipse(0 - 50, 0 -60, 30, 30);  //左耳の内側
  ellipse(0 + 50, 0 -60, 30, 30);  //右耳の内側
  fill(198, 59, 6);  //茶色
  ellipse(0, 0, 150, 150);  //顔
  fill(0, 0, 0);  //黒
  ellipse(0 - 20, 0 -20, 20, 40);  //左目
  ellipse(0 + 20, 0 -20, 20, 40);  //右目
  line(0 - 20, 0 + 30, 0 + 20, 0 + 30);  //口

}

上記コードは下記のように動作します。(画面が茶色い場合、拡大されたクマさんが画面全体を塗りつぶしている場合があります。その場合は、画面を長押しして、プログラムを再起動してみてください。)

---

クマさんの大きさとともに位置も変えるアニーメーション

下記は、クマさんがマウスを追いかけます。さらにマウスをクリックするとクマさんの大きさが変わります。拡大する場合は、キーボードで「ｂ」を押し、縮小する場合はキーボードで「s」を押します。（初期状態は拡大です）
下記プログラムには3つのポイントがあります。ひとつ目のポイントは、keyに入る値によってscParamの値を変更し、それによってクマさんの拡大、縮小の切り替えを行うことです。ふたつ目のポイントは、クマさんがマウスを追いかけるための処理です。マウスの位置がクマさんの現在位置よりも右であれば、クマさんの位置を右にずらす、マウスの位置がクマさんの現在位置よりも上であれば、クマさんの位置も上にずらす、といった処理をしています。三つ目のポイントは、kumasan()関数です。このkumasan()関数では、クマさんの中心位置と、拡大縮小のパラメーターを、引数で与えます。これによって、原点を移動し、座標の拡大縮小を行ってから、クマさんを描きます。クマさんは原点を中心に描かれるため、歪むことはありません。
プログラムを理解する最短の道は、自分で書いてみることです。初めは誰でも失敗します。失敗を克服する過程で、プログラムが理解できるようになります。だから上記の説明を理解できずとも構いません。自分のオリジナルのキャラクターを描き、それを自在に移動させるための処理を自分で考えて書いてみましょう。いつの間にか、プログラムがわかるようになっているはずです。

float sc = 1;  //拡大、縮小の初期値
float scParam = 1.01;  //拡大縮小を管理する変数
int x = width;  //クマさんの現在位置（x座標）を格納する変数
int y = height;  ////クマさんの現在位置（y座標）を格納する変数
void setup() {
  size(800, 600);
}

void draw() {
  background(200,200,200);
  kumasan(x, y, sc);

//以下、マウスを押した際にクマさんの拡大、縮小を行う処理（ポイント①）
  if(mousePressed){
    sc *=scParam;
  }
  if(key=='b'){//big
    scParam = 1.01;
  }
  if(key=='s'){//small
    scParam = 0.99;
  }

//以下、クマさんがマウスを追いかけるための処理（ポイント②）
  if(mouseX > x){
    x++;
  }
  if(mouseX < x){
    x--;
  }
  if(mouseY > y ){
    y++;
  }
  if(mouseY < y){
    y--;
  }
  
}

//クマさんを描く関数（ポイント③）
void kumasan(int tx, int ty, float sc) {
  translate(tx, ty);
  scale(sc);
  
  fill(198, 59, 6);  //茶色
  ellipse(0 - 50, 0 -60, 60, 60);  //左耳
  ellipse(0 + 50, 0 -60, 60, 60);  //右耳
  fill(250, 111, 96);  //ピンク
  ellipse(0 - 50, 0 -60, 30, 30);  //左耳の内側
  ellipse(0 + 50, 0 -60, 30, 30);  //右耳の内側
  fill(198, 59, 6);  //茶色
  ellipse(0, 0, 150, 150);  //顔
  fill(0, 0, 0);  //黒
  ellipse(0 - 20, 0 -20, 20, 40);  //左目
  ellipse(0 + 20, 0 -20, 20, 40);  //右目
  line(0 - 20, 0 + 30, 0 + 20, 0 + 30);  //口

}

上記コードは下記のように動作します。

---